
This is easy to adapt to BigInts, just do this on every limb of the number and add the appropriate offset. For example: while bitmask != 0:īitmask &= bitmask - 1 // remove lowest set bit Using the find-first-set function (or count trailing zeroes), the index of the set bit with the lowest index can be found in one step (if you accept this function as being one step, which is a reasonable assumption on most hardware, and in theory you can just define it to be one step), and then that bit can be removed so the next find-first-set will find the index of the next bit. But in the context of a machine word, there are tricks, for example based on find-first-set. mask 1 << position Then to change value of bit to b, we first make it 0 using below operation value & mask After changing it 0, we change it to b by doing or of above expression with following (b << p) & mask, i.e. For numbers known to be sparse, there is still not much that can be done - every bit has to be checked somehow because if any bit is ignored completely, that bit might have been set and we'd miss it. We first create a mask that has set bit only at given position using bit wise shift. The number of results could be as high as the number of bits anyway. Checking the bits one by one is not completely disastrous however. I will address that portion of the question.
SET BITS IN A BYTE AT SPECIFIC BIT POSITIONS HOW TO
How to calculate such positions without literally checking for bit is zero or not by going to every bit position?
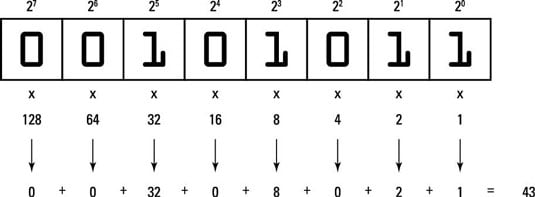
This doesn't really matter, it's easy enough to re-number the digits, but it's usually easier to follow the conventions. It also makes more sense to label that digit as "digit zero", so that the label of every digit corresponds with the exponent in the associated weight (eg bit 0 has weight 2 0=1 and so forth). In the most common convention, a binary number is written in the order as a number in other common positional representations (decimal etc): with the least significant digit in the rightmost position.


 0 kommentar(er)
0 kommentar(er)
